学習用テキスト線形計画法(9) 2次計画問題 3 と表され,2 次関数の最小化問題である.ここで,n を自然数するとき,Q ∈ Rn×n が定 数行列,c ∈ Rn が定数ベクトル,x ∈ Rn が変数ベクトルである.この問題に対して,次 の仮定を置く. 仮定1.2 正方行列Q が対称である.この映像授業では「中2 数学 1次関数1 y=ax+b」が約9分で学べます。問題を解くポイントは「yがxの1次関数は、y=ax+b」です。映像授業はTry IT(トライイット)の2次関数の問題の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の「わからない

2次関数のグラフ用紙 その2 Wordで数学問題プリントを作ろう グラフ用紙 グラフ 関数
2次関数問題 高校
2次関数問題 高校-数学 | 2次関数 Archive7 2変数関数の極値問題 7.1 復習:1変数関数の極値の求めかた F が十分に微分可能であれば2階微分までの計算で極値を求める事が出来ます: 事実7.1 十分に微分可能な関数F(t) が極値をとる可能性があるのはF′(t) = 0 で ある点のみです。



昼間から何度も質問ごめんなさい 高一の数学二次関数のグラフの問題でグラフを書く問題4 Clear
問題解説確率①~基本問題①~ 年10月30日 テーマ別解説関数をきわめよう!④ (2 次関数のグラフ) 年5月13日 テーマ別解説確率① (確率の解法) 年10月30日単元の目標 二次関数とそのグラフについて理解し,二次関数を用 いて数量の関係や変化を表現することの有用性を認識す るとともに,それらを事象の考察に活用できるようにす る。 ア 二次関数とそのグラフ「 2次関数 」カテゴリーアーカイブ 投稿ナビゲーション ← 過去の投稿
1年 比例反比例の応用 4 問題文 PがAを出発してからx秒後(誤) PがBを出発してからx秒後(正) 2年 連立方程式 解と係数 (1)問題, (3)答b=-5(誤) b=-3(正) 1年 文字式の計算2(加減)3③答 17 a → − 17 a 2年 角度2 3③130°→131°Math-Aquarium練習問題+解答2 次関数 2 2 (1) 放物線y=-2x2-14x-13 をどれだけ平行移動すると,放物線y=-2x2+8x+7 に重なるか。 (2) 2 次関数y=x2+ax+4 のグラフを,x 軸方向に2 だけ平行移動すると2 次関数y=x2-9x+b の グラフとなる。このとき,a,b の値を求めよ。たてx cm よこycmの長方形の面積が24cm 2 である。 たてxcmよこycmの長方形の周の長さが12cmである。 半径xcmの円の面積がycm 2 である。 上の問題1の(1)~(5)で1次関数はどれか。すべて答えよ。 y=3x+12 について次の問に答えよ。 x=2のときのyの値を求めよ。
2次関数の問題です。 2次関数の問題で答えは知っているのですが、途中式や解き方がわからないので困っています。 問題 (1)xの2次関数p=x^2+2kx+2k^2&#;2x&#;6k+8の最小値mは kのどのような関数になるか。中学2年生 数学 1次関数と連立方程式(文章題) 練習問題プリント 無料ダウンロード・印刷2次関数の定義域が 0≦x≦a 2次関数の最大最小値の問題で、定義域が変数で与えられている場合があります。 y=x²−4x+5 においてxの定義域が 0≦x≦aのときの最大値を求めなさい。 このような問題です。 一緒に解きながら説


大学入試数学の問題


2
中学1年生では『比例』、中学2年生では『1次関数』の式やグラフについて習いました。 3年生ではこれらをさらに発展させた『2次関数』を習います。変数が2次になっただけで、考え方自体はあまり変わりません。 ただし覚えることも増えますし、2次関数ならではのポイントもあるのでしっかり高校数学の要点, 無料の練習問題, 例題と解説 2次関数の最大と最小二次関数グラフの書き方を初めから解説! 二次関数の式の作り方をパターン別に解説! 二次関数を対称移動したときの式の求め方を解説! 平行移動したものが2点を通る式を作る方法とは? どのように平行移動したら重なる?例題を使って問題解説!



4章 二次関数 愛知県公立高校入試 数学 単元別過去問 問題プリントと解答 解説



2次関数の問題 高校数学に関する質問 勉強質問サイト
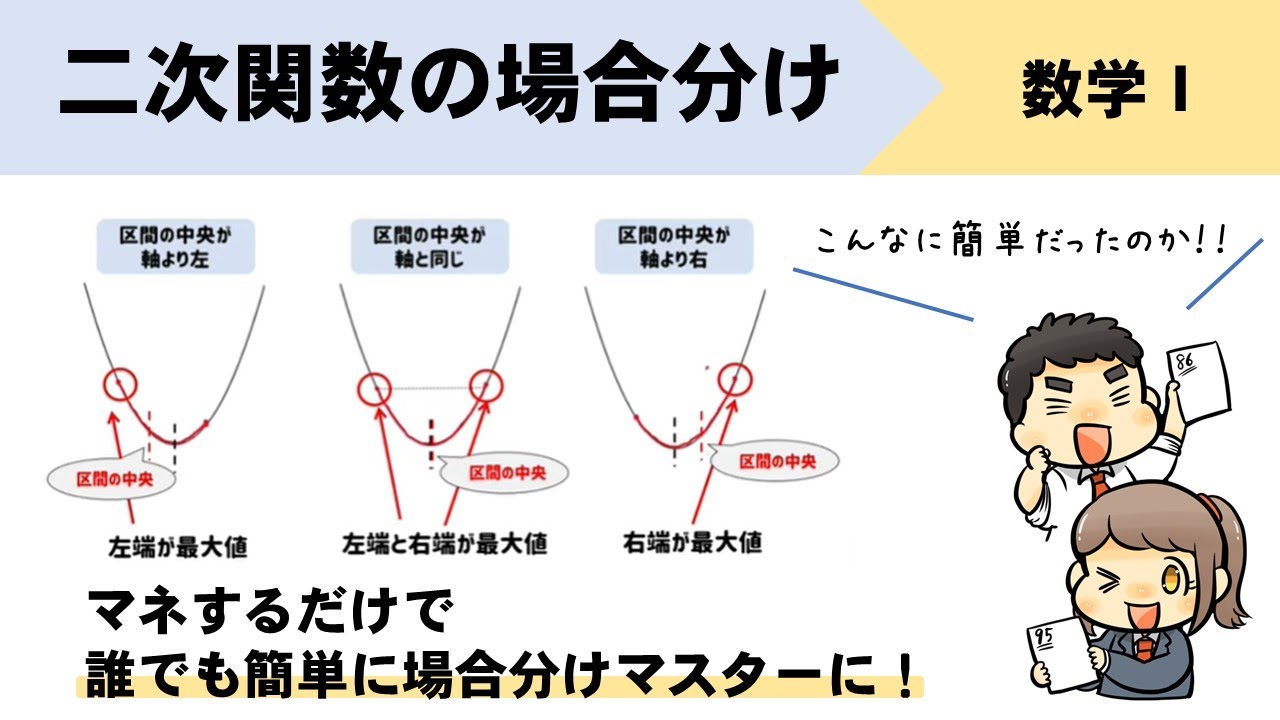
二次関数の最大値・最小値を求める問題では、「 頂点を調べること 」「 グラフを書くこと 」が最大のポイントです。 複雑な条件を考えるときでも、グラフのかたちがイメージできていれば対処できます。 基本的な問題と、場合分けが必要な問題を見てみ関数における台形の二等分線を求める練習問題です。ここで差がつく! 台形を二等分する直線は上底の中点、下底の中点を求め、それぞれを結ぶ。そのまた中点を必ず通る。 今回使う公式台形の二等分線を求める練習問題(1) DAEと DBEの面積の比を最年 東北大 後 経 1



3trial数学1 3trial数1 P38 3 2次関数の最大 最小


Www Hmg Gen Com Tecni12 3 1 Pdf
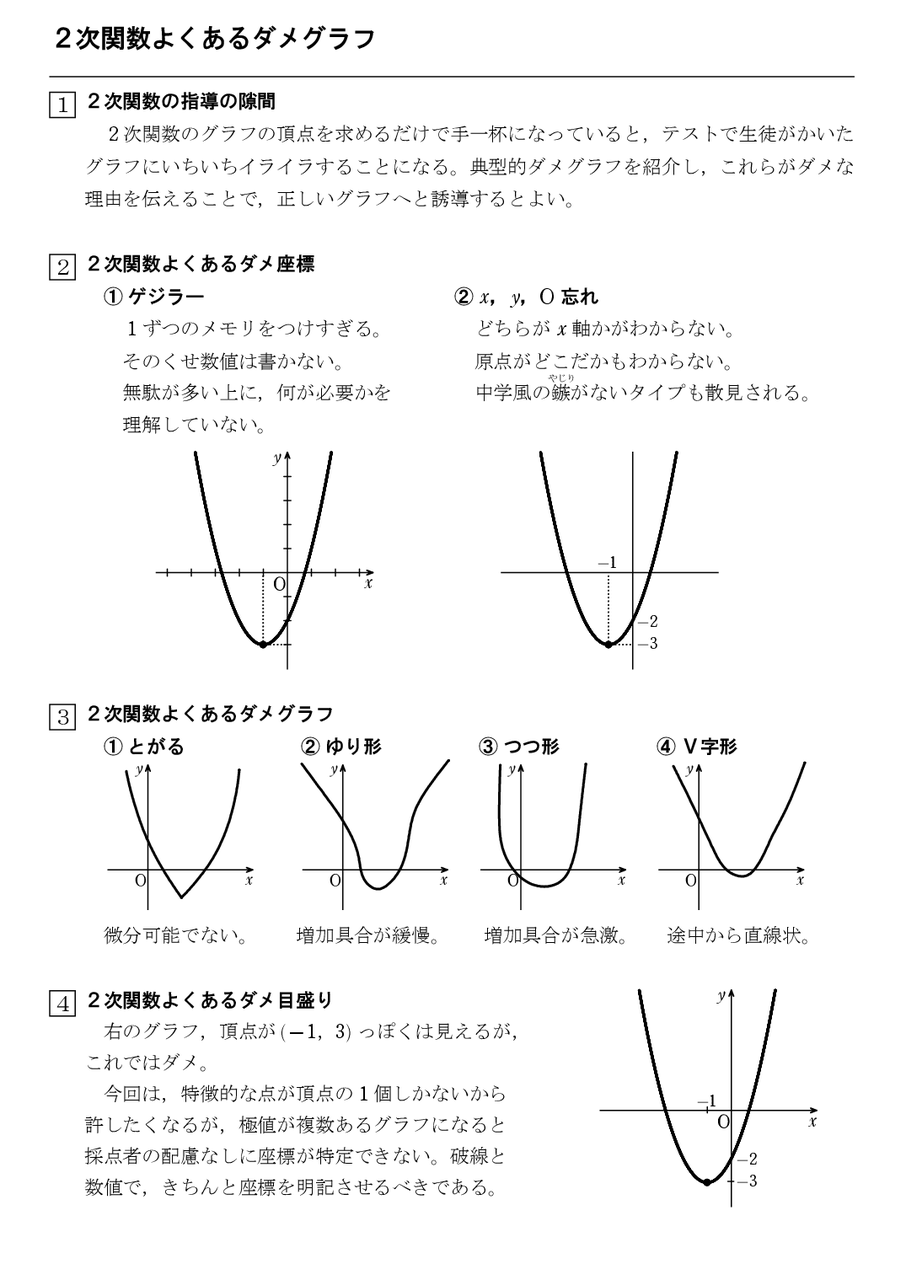
単元名 数学Ⅰ 二次関数 2.3次の問いに答えよ。 関数y=2x 2 でxの値がpからp+3まで増加するときの変化の割合が18である。 pの値を求めよ。 関数y= 1 4 x 2 でxの値がpからp+4まで増加するときの変化の割合が-2である。 pの値を求めよ。 関数y=-1 3 x 2 でxの値がpからp+8まで増加するときの変化の割合が-6である。問題3 二次関数のグラフを描くには、何個の点を明示すればよいか。 解 通過する点を任意に3個決めれば、2次関数は決定される。 頂点を明示する場合はあと1点を決めれば2次関数は決定される。結局、 (1) 任意の3点 または、 (2) 頂点と他の1点 を明示すればよい。


Http Www Hs Cuc Ac Jp Scorpion Blog Wp Content Uploads 13 10 E4 B8 E8 92 E6 Af 94 81 A E6 Ac A1 E9 96 E6 95 B0 E8 9e 8d E5 90 E5 95 8f E9 A1 8c Ef E8 E8 A3 Ef Pdf



改訂版 クリアー数学 P44 15 2次関数の最大 最小
数学3.関数 3.二次関数 4.二次関数と図形関連の複合問題 02年度問題2 1 2次関数 y=−x 2 +2x+3 のグラフを原点に関して対称に移動し,さらに x 軸方向に a , y 軸方向に b 平行移動すると頂点の座標が (1, 1) となった.このとき a= セ , b= ソ である.䑓川実地研究生が 2 次関数の活用の授業で考えた問題は、「加速するものが、一定の速度で進むものに追い つく問題」「振り子に現れる関数の問題」「図形の辺上を移動する点と面積に着目する問題」の 3 つである。



二次関数の応用 高校数学に関する質問 勉強質問サイト



二次関数 場合分け チーム エン
2次不等式 2次方程式 2次曲線 2次関数 youtube いろいろな数列 いろいろな関数の導関数 三角比 三角関数 不定積分 不等式 二項定理 円と直線 分数式の計算 剰余の定理と因数分解 双曲線 因数分解 図形と方程式 図形の面積・計量 場合の数 定積分 微分と積分 恒等式と証明 指数関数と対数関数2次関数のセンター試験問題 センター問題 3 センター問題99.1.1 センター問題 通る点→係数の決定 センター問題文字係数→最大値の最小値 センター問題 共有点の個数 2次関数の入試問題1数学Ⅰ 2次関数 復習 復習 解の公式を使う 過去問解説 大学入学共通テスト 18問題例 記述式を含む 問題例2 1 18問題例 記述式を含む 問題例1 2 18試行調査 数学ⅠA 第2問 1 18試行調査 数学ⅠA 第1問 2 17問題例 記述式を含む 問題例3 1 17問題例 記述式を含む 問題例3 2 17試行調査 数学
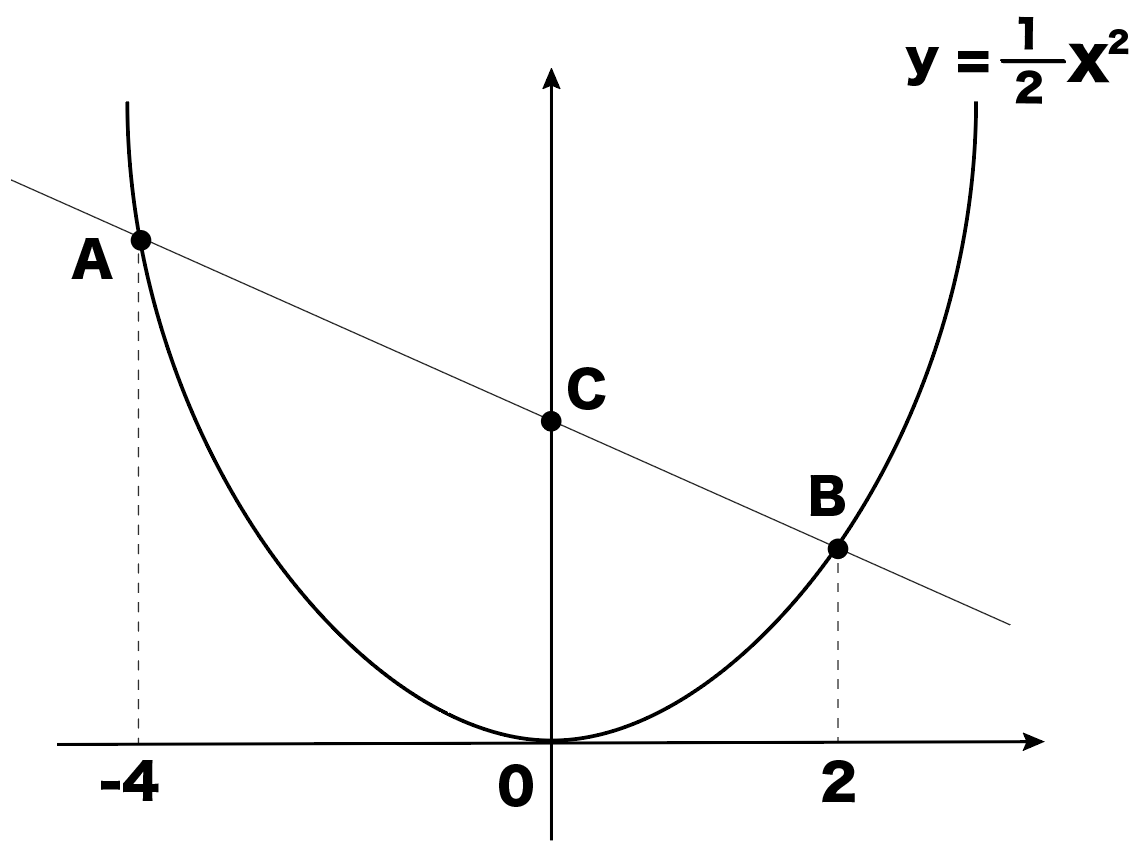


二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく
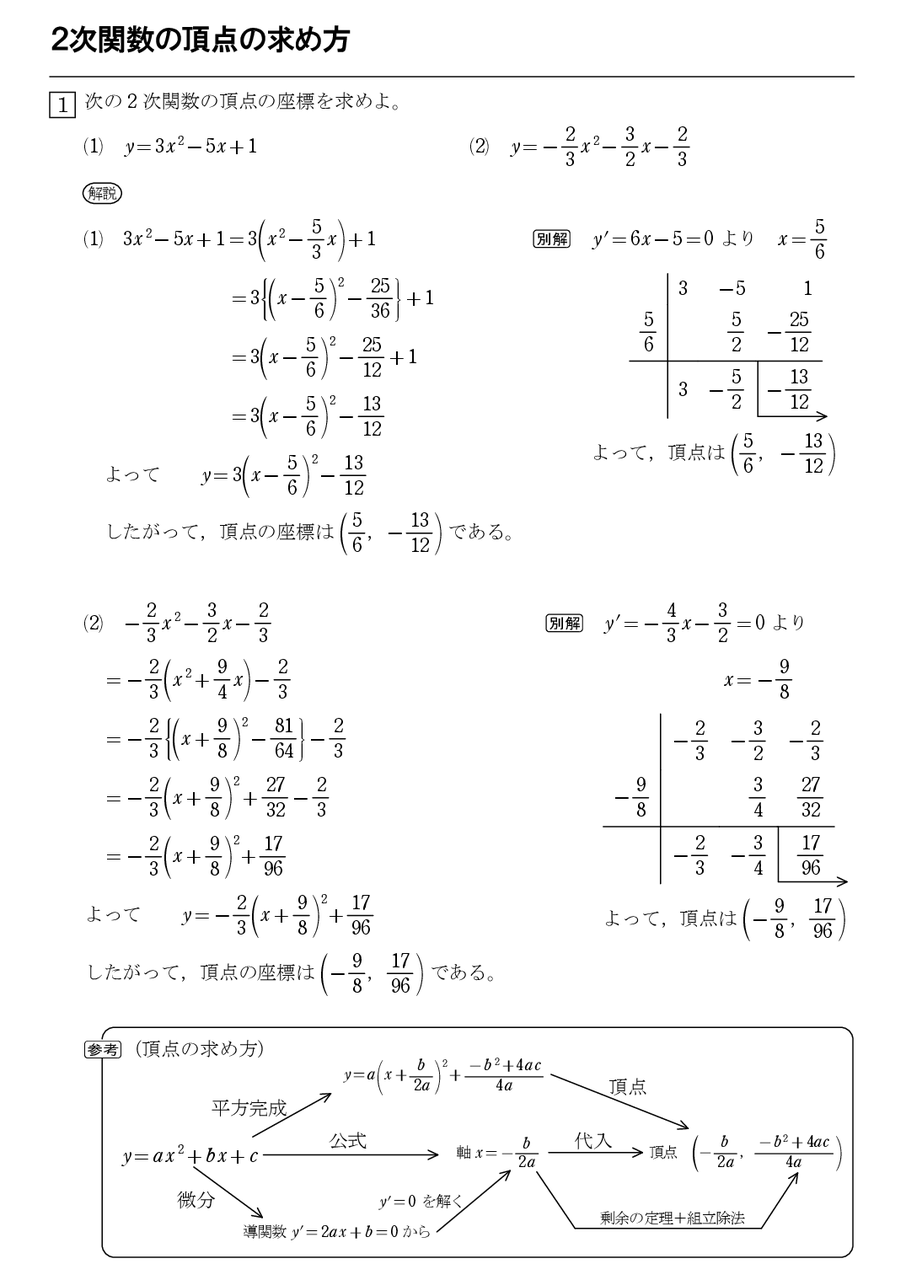


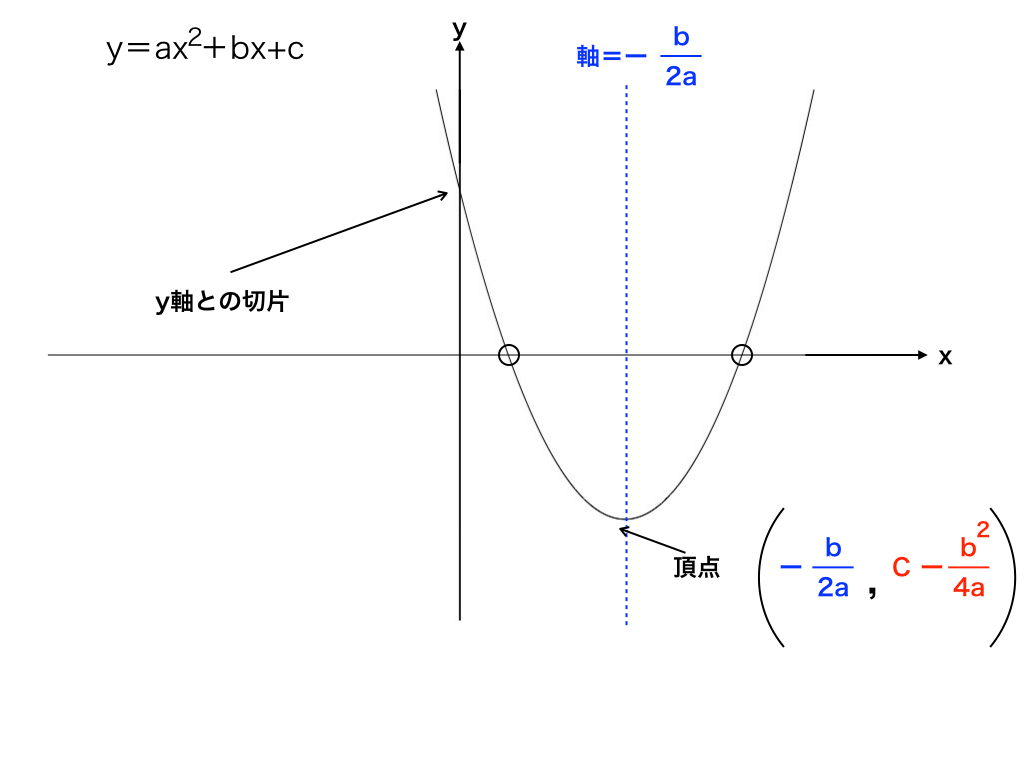
2次関数の頂点を求める別解 怜悧玲瓏 高校数学を天空から俯瞰する
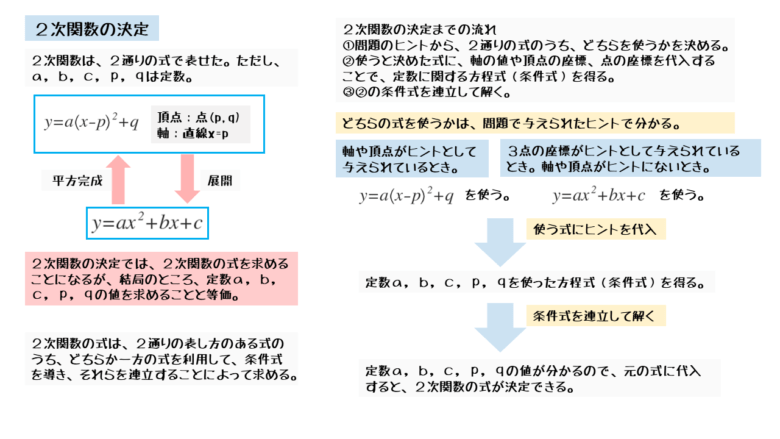
2次関数は、中学3年生で学習していく内容になる。 実際に都立入試の問題では、大問1か大問3で出題される。 では以下が実際の平成29年に出題された入試問題。 上の問題が大問1で、下の問題が大問3になる。 では、2次関数において重要になる3つのポイント問題は 二次関数y=f(x)=ax^2-(a+1)x+2a+2(a>0)があり、二次関数方程式f(x)=0の相異なる2実数解α、βが次の条件を満たすとき、αのとり得る範囲を求めます (1)α<4<β どうして、f(4)=14a-2<0 なのでしょうか?2 次関数 演習問題 14 (1) ( ) ( ) x m m m x mx m y x mx m 4 4 4 4 2 4 4 8 4 2 2 2 2 = + - + = + + = + + よって,x=-mで最小値 2 - + 4 4 m m をとる。 ゆえに, 2 =- + 4 4 l m m (2) ( )4 1 2 4 4 =- - =- + mm l m m より, l>0 であるための必要十分条件は (mm)- - > 4 1 0 すなわち (mm)- < 1 0 \ 2 2次関数のグラフ用紙 その2 Wordで数学問題プリントを作ろう グラフ用紙 グラフ 関数 変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ 中学数学単元別 2次関数 数学 中学校 教材 問題集 304 学林舎 通販 Yahoo ショッピング Www Pen Kanagawa Ed Jp Hodogaya H Documents 33nen Sougousuugaku 1 Pdf 二次関数の問題 高校数学に関する質問 勉強質問サイト 二次関数の最小値 高校数学に関する質問 勉強質問サイト 二次関数の利用の問題の解き方 グラフ無 はやさ 1 現役塾講師のわかりやすい中学数学の解き方 2次関数13 区間つき最大最小 怜悧玲瓏 高校数学を天空から俯瞰する 数学の二次関数の問題が分かりません 高校数学に関する質問 勉強質問サイト 18年 神戸学院大 栄養 薬 その他 1 数学入試問題 共通テスト 数学 自作予想問題演習 157 数学 2次関数の問題です 動点p Qで作られる三角形の面積について考えよう 三角比も用いて考えよう 苦手な人が多い分野だと思いますが 場合分けして 効率よく確実に計算しよう 高校数学 数学 2次関数 高校 受験 定期試験 数学解き方集 裏技 解法 広島経済大学 2期 16年問題3 Suugaku Jp 数学 二次関数 最小 最大値の応用問題 高校数学に関する質問 勉強質問サイト 数学 二次関数 受験問題 高校数学に関する質問 勉強質問サイト 知っ得で知っ解く二次関数 放物線 勉強法のバイブル 帝都大学へのビジョン 二次関数のグラフと解の存在範囲の問題をわかりやすく解説 48s96ub7b0z5f Net Nijikansu Max Min 3 10 6 2次関数 動点 勉強できようサイト 共通テスト モデル問題分析 数学 高校の問題集や教科教材 手帳の購入 制作なら ラーンズへ 面白い数学の問題 二次関数 たまには本格的な数学の問題を ただの大学生の雑談 受験 定期試験 数学解き方集 裏技 解法 2次関数 高校 Http Www Center Ibk Ed Jp Action Common Download Main Upload Id 5934 高校数学無料問題集 数 第2章 2次関数 グラフの利用 桝 ます Note 2次関数よくあるダメグラフ 怜悧玲瓏 高校数学を天空から俯瞰する 高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月 区間幅固定の2次関数の最大最小問題 Geogebra Warabi H Spec Ed Jp Cabinets Cabinet Files Download 459 6190d95e9c5b6fc341ec1148a7f440 Frame Id 1341 関数と図形の融合問題02 数学教材 数学の問題を作る Ketcindy Www Ajinternational Jp Struct Wp Content Uploads Ver01 Pdf センター試験 数学ia 15年問題1 Suugaku Jp 二次関数の式と値の求め方 2 現役塾講師のわかりやすい中学数学の解き方 昼間から何度も質問ごめんなさい 高一の数学二次関数のグラフの問題でグラフを書く問題4 Clear 2次方程式の解の配置問題 おいしい数学 数 二次関数 平行移動の符号はなぜ反対になるのか 答えは見方が逆だから Mm参考書 2次関数と1次関数 その1 Wordで数学問題プリントを作ろう Shoichimidorikawa Github Io Lec Basicmath2 Prob19 Pdf 楽天ブックス 大学入試 苦手対策 2次関数 三角関数 指数 対数関数 に強くなる問題集 内津 知 本 改訂版 クリアー数学 P47 15 2次関数の最大 最小 例題 2次関数の最大と最小の文章題 Youtube 01センター試験2次関数 怜悧玲瓏 高校数学を天空から俯瞰する 中学数学単元別 2次関数 数学 中学校 教材 問題集 304 学林舎 通販 Yahoo ショッピング 大学入試 苦手対策 2次関数 三角関数 指数 対数関数 に強くなる問題集 旺文社 3trial数学1 3trial数1 P45 5 2次方程式 一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく 2次関数 2次関数の決定について 日々是鍛錬 ひびこれたんれん 共通テスト 数学 自作予想問題演習 157 数学 2次関数の問題です 動点p Qで作られる三角形の面積について考えよう 三角比も用いて考えよう 苦手な人が多い分野だと思いますが 場合分けして 効率よく確実に計算しよう 高校数学 数学 超簡単 二次不等式の解き方が誰でもわかる 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ 二次関数の頻出問題を攻略 解説動画とノート付き Okenavi 高校数学 2次関数の決定 基本形 一般形 分解形 受験の月 2次関数の最大 最小 の問題のわからないを5分で解決 映像授業のtry It トライイット 大学入試共通テスト数学の裏技 2次関数の最大 最小は 頂点と区間の端を調べよ 受験の月 二次関数とは 平方完成の公式や最大値 最小値 決定の問題 受験辞典 二次関数y Axの2乗の利用問題 グラフ 中学数学に関する質問 勉強質問サイト 4章 二次関数 愛知県公立高校入試 数学 単元別過去問 問題プリントと解答 解説 数学i Aチェック リピート 第2章 2最大 最小 2 2次関数の最大 最小 Pukiwiki 高校数学 2次関数がx軸から切り取る線分の長さ 受験の月 Taro 有名問題 3 2次関数 名 2次関数の最大 最小 サクシード数学 P 改題 Http Www Fukuyamaseishikan H Hiroshima C Ed Jp Corona R0324 Math 2grade Pdf 3次曲線の対称性 至誠塾 2次関数23 2次関数の決定 怜悧玲瓏 高校数学を天空から俯瞰する Www Doshisha Ac Jp Attach Page Official Page Ja 639 File 06 bunsuu Pdf 要点 2次関数の最大と最小の文章題 Youtube 二次関数 チーム エン 楽天ブックス 大学入試 苦手対策 2次関数 三角関数 指数 対数関数 に強くなる問題集 内津 知 本 共通テスト 数学 自作予想問題演習 Twitter ನಲ ಲ 163 数学i 2次関数 集合と論理の問題です 2次関数 と座標平面上の正方形の共有点の個数について考えよう 思考力 を問うためにも いわゆる典型的な問題は減るでしょうね グラフをかいて丁寧に Www Sagami Wu Ac Jp Media Ippan Su Pdf 二次関数の場合分け 最大最小の応用問題の解き方をイチから解説 Youtube 2次関数51 解の配置レベル5の発展問題 怜悧玲瓏 高校数学を天空から俯瞰する 大学入試数学の問題 2次関数の移動に関する問題まとめ チャート 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc 大学入試 苦手対策 2次関数 三角関数 指数 対数関数 に強くなる問題集 旺文社 中学3年生 数学 2学期 中間テスト 練習問題 2次方程式 2次関数 赤城の裾野 数学コーナー 高校3年 数学i A センター試験対策練習問題 2次関数だよ 赤城の裾野 2次関数と1次関数がつくる三角形 Wordで数学問題プリントを作ろう 4次関数と2次関数とで囲まれる図形の面積 2020年度後期日程の東北大学理学部 経済学部 理系 入試 身勝手な主張 高校1年の二次関数 最大値 最小値を求める問題です Clear 2 演習問題 2次関数 Y A X P 2 のグラフ Youtube 無料ダウンロード 中学二次関数問題 印刷とダウンロードは無料 二次関数の問題です なぜ 2だけ平行移動するときにy 2になるかが分かりません Clear 数学コーナー 無料 中3数学 高校入試対策問題 問題プリント 315 関数4 2次関数の練習問題 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc 中学数学単元別 2次関数 数学 中学校 教材 問題集 304 学林舎 通販 Yahoo ショッピング








































































































































































































































0 件のコメント:
コメントを投稿